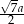/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 3986298

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawa trójkąta równoramiennego i środkowe poprowadzone z jej konców mają długość a . Oblicz długość wysokości poprowadzonej do podstawy.

Rozwiązanie

Zaczynamy od rysunku.

PIC

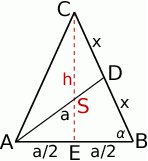
Sposób I

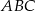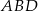Zauważmy, że trójkąty ABC i ABD oba są równoramienne oraz mają wspólny kąt 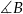∡B przy podstawie. Są one zatem podobne. Jeżeli oznaczymy długość ramienia 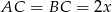AC = BC = 2x , to z podobieństwa mamy

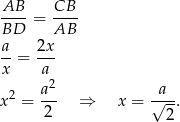
AB-- CB-- BD = AB a 2x --= --- x a 2 a2- -a-- x = 2 ⇒ x = √ 2-.

Szukaną długość wysokośći liczymy z twierdzenia Pitagorasa.

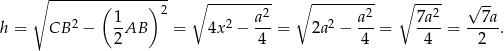
∘ ----------------- ( ) 2 ∘ -------2- ∘ --------2 ∘ ---2 √ -- h = CB 2 − 1AB = 4x2 − a--= 2a2 − a--= 7a-- = --7a-. 2 4 4 4 2

Sposób II

Tym razem skorzystamy z tego, że środkowe w trójkącie dzielą się w stosunku 2:1. Mamy zatem

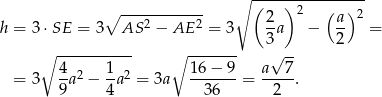
∘ (----)2--------- ∘ ----2------2 2- ( a) 2 h = 3 ⋅SE = 3 AS − AE = 3 3 a − 2 = ∘ ----------- ∘ ------- √ -- 4-2 1- 2 16-−-9- a--7- = 3 9a − 4 a = 3a 36 = 2 .

 
Odpowiedź: √ - --7a 2

Wersja PDF