Zadanie nr 4039750

W pewnym trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 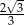√ - 2--3 3 . Oblicz iloczyn sinusów tych kątów.

Rozwiązanie

Naszkicujmy trójkąt prostokątny.

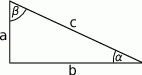
Sposób I

Z obrazka widzimy, że

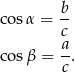
b- cos α = c a cos β = --. c

Zatem wiemy, że

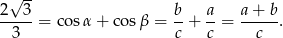
√ -- 2 3 b a a+ b -----= co sα + cos β = -+ --= -----. 3 c c c

Podnosimy teraz tę równość stronami do kwadratu i korzystamy z twierdzenia Pitagorasa.

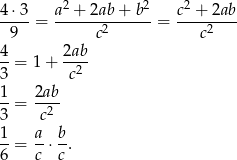
4⋅ 3 a2 + 2ab + b2 c2 + 2ab ---- = --------------= --------- 9 c2 c2 4- 2ab- 3 = 1 + c2 1 2ab --= -2-- 3 c 1-= a⋅ b. 6 c c

Teraz pozostało zauważyć, że z prawej strony otrzymaliśmy dokładnie iloczyn sinusów:

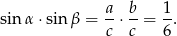
sinα ⋅sinβ = a-⋅ b-= 1. c c 6

Sposób II

Tym razem skorzystajmy z równości 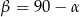β = 90 − α . Mamy więc

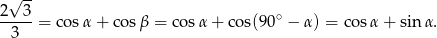
√ -- 2 3 -----= cos α+ cosβ = cosα + co s(90∘ − α) = cos α+ sin α. 3

Podnosimy tę równość stronami do kwadratu i korzystamy z jedynki trygonometrycznej.

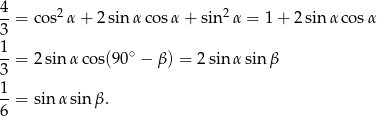
4- 2 2 3 = cos α + 2sinα cos α+ sin α = 1 + 2 sinα cos α 1 --= 2sin αco s(90∘ − β) = 2 sin α sin β 3 1-= sinα sinβ . 6

Odpowiedź: 1 6