/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 4256113

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wartości funkcji trygonometrycznych kątów ostrych trójkąta powstałego wskutek połączenia odcinkiem wierzchołka kwadratu ze środkiem przeciwległego boku.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

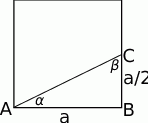
Najpierw, korzystając z twierdzenia Pitagorasa, wyliczmy długość boku 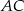AC .

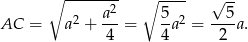
∘ -------- ∘ ---- √ -- 2 a2- 5- 2 --5- AC = a + 4 = 4a = 2 a.

Możemy teraz policzyć żądane funkcje trygonometryczne

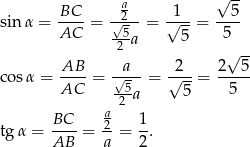
√ -- BC a 1 5 sinα = ----= √-2- = √---= ---- AC -25a 5 5 √ -- cos α = AB-- = -√a- = √2--= 2--5- AC -5a 5 5 a 2 tgα = BC--= 2-= 1. AB a 2

Podobnie wyliczamy funkcje trygonometryczne kąta 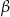β , wyjdzie nam

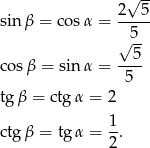
√ -- sin β = cosα = 2--5- 5 √ 5- cosβ = sinα = ---- 5 tgβ = ctg α = 2 1 ctgβ = tg α = -. 2

 
Odpowiedź: √- √ - sin β = cosα = 255, cos β = sinα = -55, tg β = ctg α = 2

Wersja PDF