/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 4279608

Dodaj do ulubionych
Dodaj do rozwiązanych

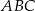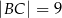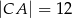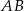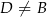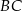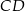W trójkącie prostokątnym ABC przyprostokątne mają długości: |BC | = 9 , |CA | = 12 . Na boku AB wybrano punkt D ⁄= B tak, że odcinki BC i CD mają równe długości. Oblicz długość odcinka AD .

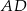Rozwiązanie

Zadanie ma wiele możliwych rozwiązań, my pokażemy trzy z nich.

Sposób I

PIC

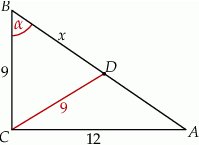
Obliczmy najpierw długość przeciwprostokątnej.

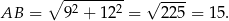
∘ --------- √ ---- AB = 92 + 122 = 22 5 = 15.

Wystarczy, że obliczymy długość odcinka 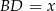BD = x . Możemy to łatwo zrobić z twierdzenia cosinusów w trójkącie CDB .

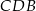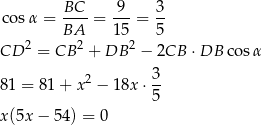
co sα = BC--= 9--= 3- BA 15 5 CD 2 = CB 2 + DB 2 − 2CB ⋅DB cos α 81 = 8 1+ x 2 − 1 8x⋅ 3 5 x(5x − 54 ) = 0

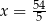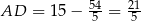Stąd x = 54- 5 oraz AD = 15 − 54 = 21 5 5 .

Sposób II

W zasadzie jest to mała modyfikacja poprzedniego sposobu.

PIC

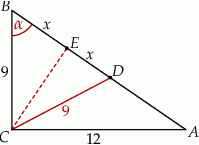
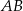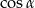Podobnie jak poprzednio wyliczamy AB i cos α . Ponieważ trójkąt 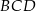BCD jest równoramienny, to jeżeli narysujemy jego wysokość 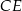CE i oznaczymy 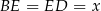BE = ED = x , to mamy

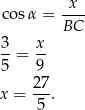
x co sα = ---- BC 3-= x- 5 9 27 x = --. 5

Stąd 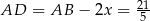AD = AB − 2x = 21 5 .

Sposób III

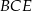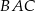Wykorzystamy rysunek z poprzedniego podpunktu. Trójkąty BCE i BAC są podobne, więc

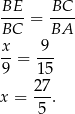
BE BC ----= ---- BC BA x- 9-- 9 = 15 2 7 x = ---. 5

Dalej, jak poprzednio 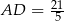21 AD = 5 .  
Odpowiedź: 21 AD = -5

Wersja PDF