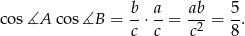Zadanie nr 4605280
W trójkącie prostokątnym suma sinusów kątów ostrych jest równa  . Wykaż, że iloczyn cosinusów tych kątów jest równy
. Wykaż, że iloczyn cosinusów tych kątów jest równy  .
.
Rozwiązanie
Sposób I
Jeżeli  jest kątem ostrym trójkąta prostokątnego, to drugi kąt ostry ma miarę
jest kątem ostrym trójkąta prostokątnego, to drugi kąt ostry ma miarę 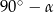 . Mamy więc równanie
. Mamy więc równanie
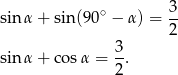
Podnieśmy tę ostatnią równość stronami do kwadratu.
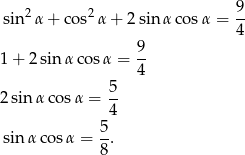
Zauważmy teraz, że interesujący nas iloczyn cosinusów jest równy
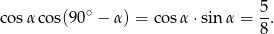
Sposób II
Oznaczmy długości przyprostokątnych trójkąta przez  i
i 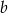 , a długość przeciwprostokątnej przez
, a długość przeciwprostokątnej przez  .
.
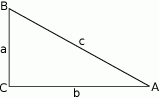
Mamy zatem
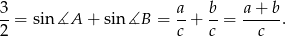
Podnosimy tę równość stronami do kwadratu (żeby skorzystać z twierdzenia Pitagorasa).
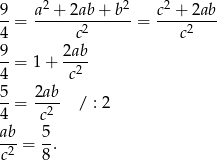
Teraz pozostało zauważyć, że