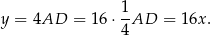Zadanie nr 4623086
W trójkącie prostokątnym jedna przyprostokątna jest 4 razy dłuższa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 16 razy dłuższy od drugiego.
Rozwiązanie
Zaczynamy od rysunku
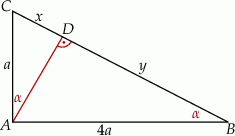
Zauważmy, że trójkąty 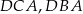 są podobne do trójkąta
są podobne do trójkąta 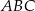 (bo mają z tym trójkątem dwa kąty wspólne).
(bo mają z tym trójkątem dwa kąty wspólne).
Sposób I
Korzystając z zauważonego podobieństwa mamy
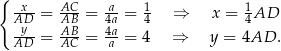
Stąd
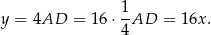
Sposób II
Jeżeli oznaczymy 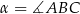 , to
, to
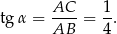
Patrzymy teraz na trójkąty 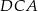 i
i 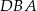 .
.
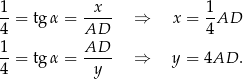
Stąd