Zadanie nr 4781570
Środek okręgu opisanego na trójkącie prostokątnym leży w odległości 3 cm i 2 cm od przyprostokątnych. Oblicz pole tego trójkąta.
Rozwiązanie
Zaczynamy od rysunku.
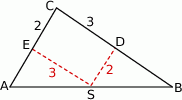
Ponieważ średnicą okręgu opisanego na trójkącie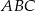 
jest przeciwprostokątna 
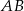(bo 
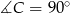), więc środek 
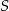okręgu opisanego na tym trójkącie to dokładnie środek przeciwprostokątnej. Jeżel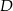i 
i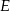 
są rzutami 
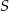na bok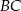i 
i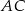 
, to na mocy twierdzenia Talesa, punkty 
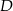i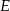 
są środkami tych boków. Zatem
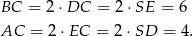
Pole jest więc równe
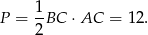
Odpowiedź: 
