/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 4886563

Dodaj do ulubionych
Dodaj do rozwiązanych

Środkowa 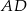AD trójkąta równoramiennego 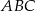ABC ma długość 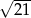√ --- 21 , a jego podstawa 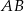AB tworzy z ramieniem kąt o mierze 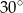30∘ . Oblicz pole trójkąta ABC .

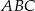Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

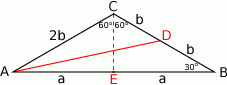
Sposób I

Oznaczmy długość ramienia trójkąta przez 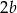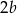2b (2b , a nie 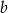b , żeby mieć trochę mniej ułamków). Liczbę 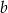b możemy wyznaczyć pisząc twierdzenie cosinusów w trójkącie ADC . Liczymy

AD 2 = AC 2 + DC 2 − 2AC ⋅DC cos ∡ 120∘ ( ) 21 = 4b 2 + b2 − 2 ⋅2b ⋅b⋅ − 1- 2 2 2 21 = 5b + 2b 21 = 7b 2 / : 7 2 √ -- b = 3 ⇒ b = 3.

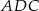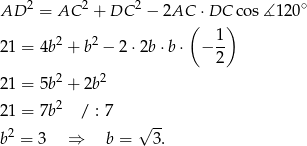
Liczymy teraz pole trójkąta 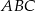ABC korzystając ze wzoru z sinusem.

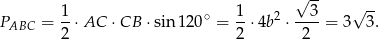
√ -- 1- ∘ 1- 2 --3- √ -- PABC = 2 ⋅AC ⋅CB ⋅sin 120 = 2 ⋅4b ⋅ 2 = 3 3.

Sposób II

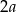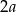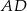Oznaczmy długość podstawy trójkąta przez 2a (2a , a nie a , żeby mieć trochę mniej ułamków). Informację o długości środkowej AD będziemy chcieli wykorzystać pisząc twierdzenie cosinusów w trójkącie 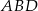ABD . Zanim to jednak zrobimy, obliczmy długość odcinka BD .

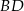Z trójkąta prostokątnego 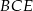BCE mamy

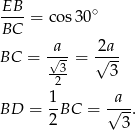
EB-- ∘ BC = co s30 a 2a BC = √-- = √--- -23 3 1 a BD = --BC = √---. 2 3

Piszemy teraz twierdzenie cosinusów w trójkącie 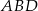ABD .

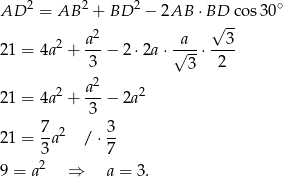
2 2 2 ∘ AD = AB + BD − 2AB ⋅BD-co s30 a2 a √ 3 21 = 4a2 + ---− 2 ⋅2a ⋅√---⋅---- 3 3 2 2 a2 2 21 = 4a + ---− 2a 3 21 = 7-a2 / ⋅ 3 3 7 9 = a2 ⇒ a = 3.

Jeszcze raz patrzymy na trójkąt prostokątny 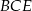BCE .

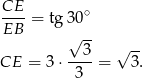
CE ----= tg30 ∘ EB √ -- --3- √ -- CE = 3 ⋅ 3 = 3.

Pole trójkąta jest więc równe

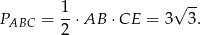
-- P = 1⋅ AB ⋅ CE = 3√ 3. ABC 2

 
Odpowiedź: √ -- 3 3

Wersja PDF