Zadanie nr 4945084
Wykaż, że jeżeli 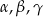 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 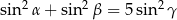 , to
, to 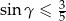 .
.
Rozwiązanie
Szkicujemy trójkąt.
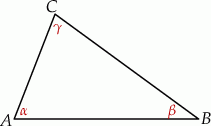
Korzystając z twierdzenia sinusów
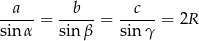
możemy zamienić sinusy w danej równości na długości boków trójkąta.
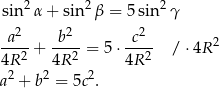
Teraz korzystając z twierdzenia cosinusów
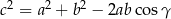
rozpisujemy 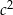
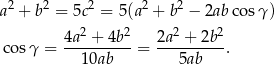
Stąd
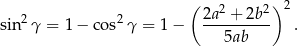
Wystarczy teraz udowodnić, że 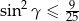 . Przekształcamy tę nierówność w sposób równoważny.
. Przekształcamy tę nierówność w sposób równoważny.
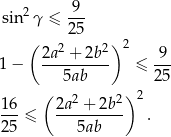
Po obu stronach mamy kwadraty liczb dodatnich, więc wystarczy udowodnić, że
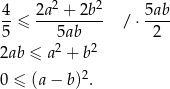
Otrzymana nierówność jest oczywiście prawdziwa, więc wyjściowa nierówność też musiała być prawdziwa.

