Zadanie nr 5296790
Wykaż, że jeżeli środkowa trójkąta jest dwa razy krótsza od boku, do którego jest poprowadzona, to trójkąt ten jest prostokątny.
Rozwiązanie
Niech 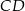 będzie taką środkową trójkąta
będzie taką środkową trójkąta 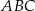 , dla której
, dla której 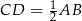 .
.
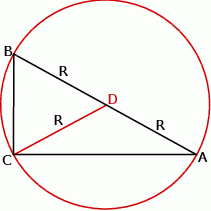
Ponieważ 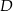 jest środkiem odcinka
jest środkiem odcinka 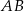 , mamy stąd
, mamy stąd
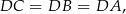
czyli punkty 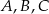 leżą na okręgu o środku
leżą na okręgu o środku 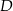 i promieniu
i promieniu 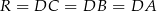 . Ponadto, odcinek
. Ponadto, odcinek 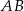 jest średnicą tego okręgu, więc
jest średnicą tego okręgu, więc
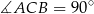
(kąt oparty na średnicy).

