Zadanie nr 5303304
Punkt 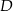 leży na boku
leży na boku 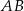 trójkąta
trójkąta 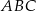 oraz
oraz 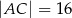 ,
, 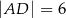 ,
, 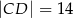 i
i 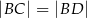 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 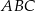 .
.
Rozwiązanie
Narysujmy opisaną sytuację.
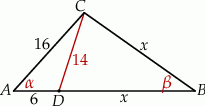
Sposób I
Piszemy twierdzenia cosinusów w trójkątach 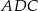 i
i 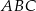 .
.
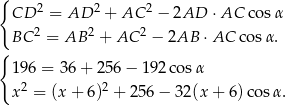
Z pierwszego równania mamy
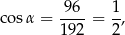
czyli 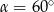 . Drugie równanie przyjmuje więc postać
. Drugie równanie przyjmuje więc postać
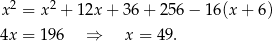
Obwód trójkąta 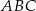 jest więc równy
jest więc równy
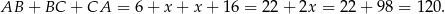
Sposób II
Piszemy twierdzenia cosinusów w trójkątach 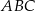 i
i 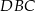 .
.
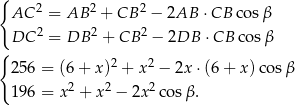
Podstawiamy teraz 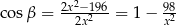 z drugiego równania do pierwszego
z drugiego równania do pierwszego
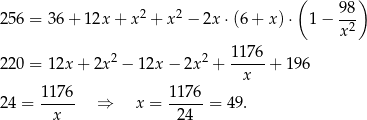
Obwód trójkąta 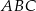 jest więc równy
jest więc równy
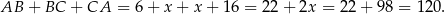
Odpowiedź: 120

