/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 5467873

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie prostokątnym 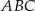ABC jedna z przyprostokątnych jest o 7 dłuższa od drugiej, a promień okręgu wpisanego w ten trójkąt jest równy 3. Oblicz obwód trójkąta ABC .

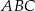Rozwiązanie

Szkicujemy trójkąt prostokątny.

PIC

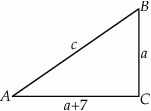
Korzystamy ze wzoru

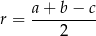
r = a+--b−-c- 2

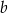na promień r okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości a i b oraz przeciwprostokątnej długości c . Mamy więc

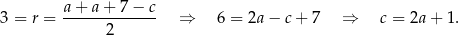
3 = r = a-+-a-+-7−--c ⇒ 6 = 2a − c+ 7 ⇒ c = 2a+ 1. 2

Ponadto, na mocy twierdzenia Pitagorasa

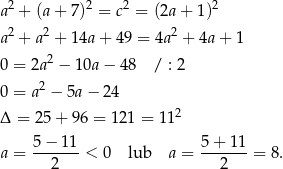
a 2 + (a + 7)2 = c2 = (2a+ 1)2 2 2 2 a + a + 14a + 49 = 4a + 4a + 1 2 0 = 2a − 10a − 48 / : 2 0 = a2 − 5a− 24 2 Δ = 25 + 96 = 121 = 1 1 5 − 11 5 + 11 a = -------< 0 lub a = -------= 8. 2 2

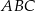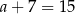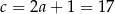Pozostałe boki trójkąta ABC mają więc długości: a + 7 = 15 i c = 2a + 1 = 17 . Obwód trójkąta jest równy

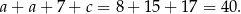
a + a + 7 + c = 8 + 15 + 17 = 40.

 
Odpowiedź: 40

Wersja PDF