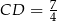/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 5650062

Dodaj do ulubionych
Dodaj do rozwiązanych

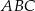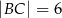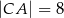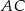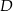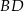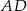W trójkącie prostokątnym ABC przyprostokątne mają długości: |BC | = 6 , |CA | = 8 . Na boku AC wybrano punkt D tak, że odcinki BD i AD mają równe długości. Oblicz długość odcinka CD .

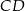Rozwiązanie

Zaczynamy od rysunku.

PIC

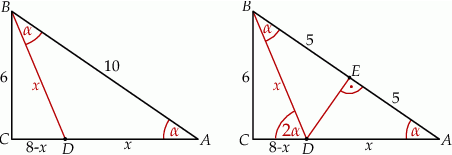
Oznaczmy 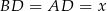BD = AD = x . Oczywiście wystarczy wyliczyć x . Zacznijmy od wyliczenia długości przeciwprostokątnej.

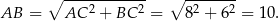
∘ ------------ ∘ ------- AB = AC 2 + BC 2 = 82 + 62 = 1 0.

Sposób I

Napiszemy twierdzenie cosinusów w trójkącie 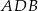ADB . Ponieważ

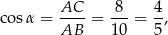
AC 8 4 co sα = ----= ---= -, AB 10 5

mamy

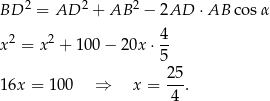
2 2 2 BD = AD + AB − 2AD ⋅AB cosα 2 2 4- x = x + 100 − 20x ⋅5 2 5 1 6x = 100 ⇒ x = ---. 4

Stąd

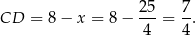
25 7 CD = 8 − x = 8 − ---= -. 4 4

Sposób II

Napiszmy twierdzenie Pitagorasa w trójkącie 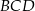BCD .

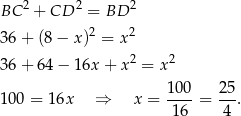
BC 2 + CD 2 = BD 2 2 2 3 6+ (8 − x ) = x 3 6+ 6 4− 16x + x2 = x 2 1 00 = 16x ⇒ x = 1-00 = 2-5. 16 4

Długość odcinka 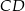CD wyliczamy jak poprzednio.

Sposób III

Jeżeli dorysujemy wysokość 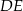DE w trójkącie 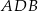ADB to mamy

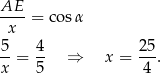
AE ----= cosα x 5-= 4- ⇒ x = 25-. x 5 4

Długość odcinka 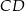CD wyliczamy jak poprzednio.

Sposób IV

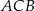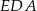Możemy też się obyć bez trygonometrii. Trójkąty ACB i EDA są oba prostokątne i mają wspólny kąt, więc są podobne. Zatem

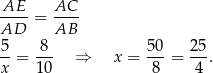
-AE- = AC-- AD AB 5 8 50 25 -- = --- ⇒ x = ---= --. x 10 8 4

Długość odcinka 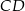CD wyliczamy jak poprzednio.

Sposób V

Tym razem wyliczmy długość odcinka 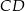CD bezpośrednio. Patrzymy na trójkąt prostokątny CDB .

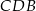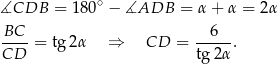
∘ ∡CDB = 180 − ∡ADB = α + α = 2α BC-- --6-- CD = tg2 α ⇒ CD = tg2α .

Musimy więc wyliczyć 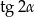tg 2α . Jest na to gotowy wzorek (z tablic)

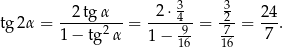
2 tgα 2⋅ 3 3 2 4 tg 2α = ------2--= ----49--= 27--= ---. 1− tg α 1− 16 16 7

Mamy więc

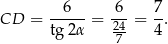
6 6 7 CD = ----- = 24-= -. tg 2α 7- 4

 
Odpowiedź: CD = 7 4

Wersja PDF