/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 5928314

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że jeżeli kąty 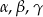α,β ,γ trójkąta 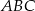ABC spełniają warunek 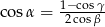1−cosγ- cos α = 2cosβ to trójkąt jest równoramienny.

Rozwiązanie

Przekształcamy podany warunek korzystając z tego, że 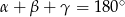∘ α+ β+ γ = 1 80 .

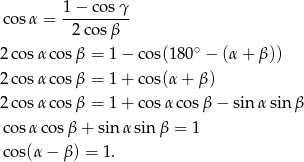
1− cosγ cosα = ---------- 2 cosβ 2 cosα cos β = 1 − cos(18 0∘ − (α + β)) 2 cosα cos β = 1 + cos(α + β ) 2 cosα cos β = 1 + cos αco sβ − sinα sinβ cosα cosβ + sin α sin β = 1 cos(α− β) = 1.

Ponieważ 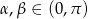α ,β ∈ (0,π ) jedynym rozwiązaniem tego równania jest 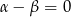α− β = 0 , co oczywiście oznacza, że trójkąt jest równoramienny.

Wersja PDF