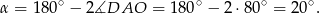/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 5978210

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą trójkąta równoramiennego 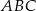ABC jest średnica 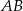AB okręgu, którego środkiem jest punkt 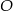O . Punkty 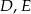D ,E są punktami przecięcia ramion 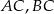AC ,BC trójkąta z okręgiem. Miara kąta 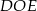DOE jest równa 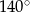140 ∘ . Wykaż, że miara kąta 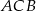ACB jest równa 20∘ .

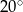Rozwiązanie

Zaczynamy od rysunku

PIC

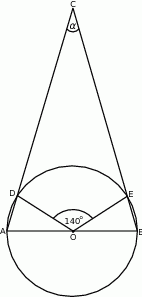
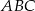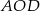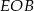Po pierwsze zauważmy, że ponieważ trójkąt ABC jest równoramienny, więc trójkąty AOD i EOB są przystające. Liczymy

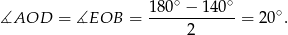
∘ ∘ ∡AOD = ∡EOB = 180--−-140--= 20∘. 2

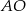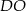Odcinki AO i DO mają równe długości (bo są promieniami okręgu), więc trójkąt 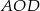AOD jest równoramienny. Zatem

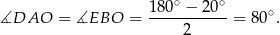
∘ ∘ ∡DAO = ∡EBO = 180--−-2-0- = 80∘. 2

Ponieważ 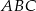ABC jest równoramienny, więc

α = 180∘ − 2∡DAO = 1 80∘ − 2⋅8 0∘ = 20∘.
Wersja PDF