Zadanie nr 6009899
Punkty 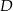 i
i 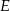 są takimi punktami przeciwprostokątnej
są takimi punktami przeciwprostokątnej 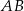 trójkąta prostokątnego
trójkąta prostokątnego 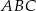 , że
, że 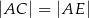 i
i 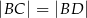 . Wykaż, że
. Wykaż, że 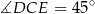 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
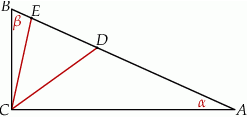
Wiemy, że trójkąt 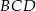 jest równoramienny, więc
jest równoramienny, więc
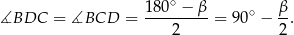
Równoramienny jest też trójkąt 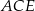 , więc
, więc
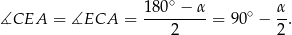
Patrzymy teraz na trójkąt 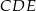 .
.