Zadanie nr 6042672
Punkt 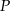 należy do boku
należy do boku 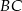 trójkąta równobocznego
trójkąta równobocznego 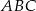 . Odcinek
. Odcinek 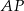 ma długość 6 i tworzy z bokiem
ma długość 6 i tworzy z bokiem 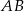 kąt
kąt 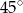 . Oblicz pole trójkąta
. Oblicz pole trójkąta 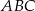 .
.
Rozwiązanie
Zaczynamy od rysunku.
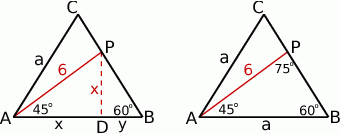
Sposób I
Niech 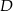 będzie rzutem punktu
będzie rzutem punktu 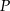 na bo
na bo 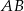 oraz
oraz 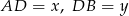 . Zauważmy, że trójkąt
. Zauważmy, że trójkąt 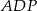 jest równoramiennym trójkątem prostokątnym (jest to połówka kwadratu), więc
jest równoramiennym trójkątem prostokątnym (jest to połówka kwadratu), więc
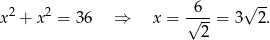
Z trójkąta prostokątnego 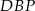 obliczamy
obliczamy 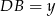 .
.
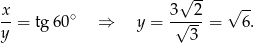
W takim razie bok trójkąta ma długość
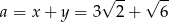
i pole jest równe
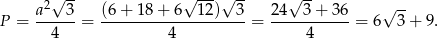
Sposób II
Bok trójkąta możemy łatwo wyliczyć z twierdzenia sinusów w trójkącie 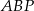 . Aby to zrobić policzmy najpierw
. Aby to zrobić policzmy najpierw 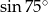 .
.
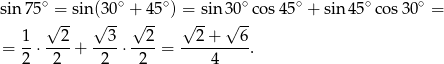
Stosujemy teraz twierdzenie sinusów w trójkącie 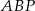 .
.
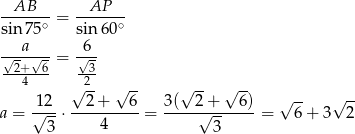
Zatem pole jest równe
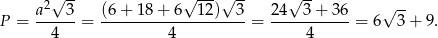
Odpowiedź: