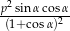/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 6135371

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równoramiennym dany jest obwód 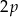2p oraz miara kąta przy podstawie α . Oblicz pole powierzchni tego trójkąta.

Rozwiązanie

Zaczynamy od rysunku.

PIC

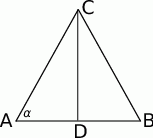
Z trójkąta prostokątnego 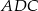ADC mamy

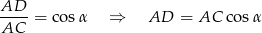
AD-- = co sα ⇒ AD = AC cos α AC

oraz

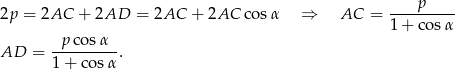
p 2p = 2AC + 2AD = 2AC + 2AC cos α ⇒ AC = --------- p cosα 1 + cos α AD = ---------. 1 + cos α

Ponadto

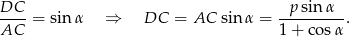
DC-- = sinα ⇒ DC = AC sin α = --psin-α-. AC 1 + co sα

Zatem pole trójkąta jest równe

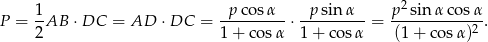
2 1- -p-cosα-- -p-sin-α-- p--sin-α-cosα- P = 2 AB ⋅DC = AD ⋅DC = 1+ cosα ⋅ 1+ cosα = (1 + co sα)2 .

 
Odpowiedź: p2sinαcosα -(1+cosα)2-

Wersja PDF