Zadanie nr 6175618
Dany jest trójkąt prostokątny 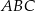 , w którym
, w którym 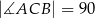 i
i 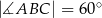 . Niech
. Niech 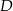 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 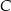 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 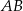 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 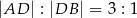 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
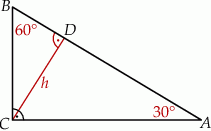
Jeżeli oznaczymy 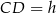 , to w trójkątach prostokątnych
, to w trójkątach prostokątnych 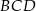 i
i 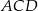 mamy
mamy
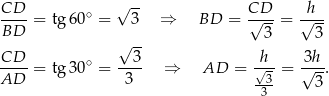
Zatem rzeczywiście 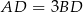 .
.

