Zadanie nr 6379809
W ostrokątnym trójkącie równoramiennym ramię ma długość 61, a wysokość poprowadzona do ramienia ma długość 11. Oblicz długość podstawy tego trójkąta.
Rozwiązanie
Zaczynamy oczywiście od szkicowego rysunku.
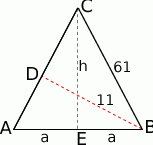
Sposób I
Oznaczmy szukaną długość podstawy przez 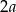 (
(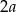 , a nie
, a nie  żeby nie mieć ułamków) i zauważmy, że możemy na dwa sposoby obliczyć pole trójkąta
żeby nie mieć ułamków) i zauważmy, że możemy na dwa sposoby obliczyć pole trójkąta 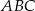 .
.
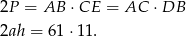
Potrzebujemy jeszcze drugie równanie – dostajemy je z trójkąta prostokątnego 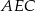 .
.
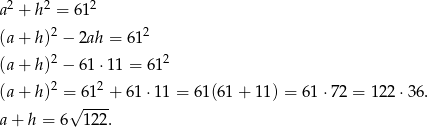
Mamy zatem układ równań
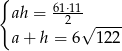
Układ ten możemy rozwiązać standardowo, lub zauważyć, że na mocy wzorów Viète’a rozwiązania tego układu są pierwiastkami równania
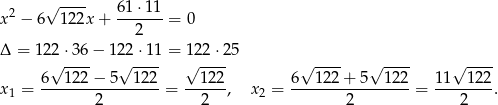
Pozostało ustalić, która z tych liczb to  , a która to
, a która to 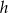 . Gdyby było
. Gdyby było 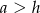 , to
, to 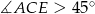 i kąt przy wierzchołku
i kąt przy wierzchołku 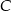 byłby rozwarty. Zatem
byłby rozwarty. Zatem 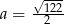 i podstawa ma długość
i podstawa ma długość 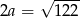 .
.
Sposób II
Tym razem będziemy odrobinę bardziej pomysłowi i policzymy długość odcinka 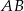 wprost. Jak to zrobić? – z trójkąta prostokątnego
wprost. Jak to zrobić? – z trójkąta prostokątnego 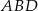 . Aby móc to jednak zrobić musimy najpierw wyliczyć długość odcinka
. Aby móc to jednak zrobić musimy najpierw wyliczyć długość odcinka 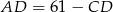 . Patrzymy na trójkąt prostokątny
. Patrzymy na trójkąt prostokątny 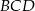 i liczymy
i liczymy
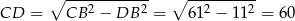
Zatem 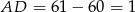 oraz
oraz
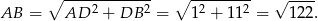
Odpowiedź: