/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 6526250

Dodaj do ulubionych
Dodaj do rozwiązanych

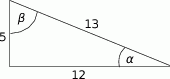
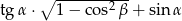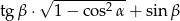Na rysunku oznaczono kąty oraz podano długości boków trójkąta prostokątnego. Oblicz, które z wyrażeń ma większą wartość: ∘ ---------- tgα ⋅ 1− co s2β + sin α czy √ ---------- tg β ⋅ 1 − cos2 α+ sin β .

PIC

Rozwiązanie

Spróbujmy przekształcić podane wyrażenie

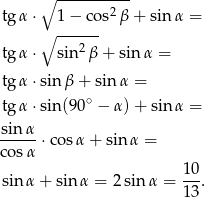
∘ ---------- tg α⋅ 1− cos2β + sin α = ∘ ------ tg α⋅ sin 2β + sin α = tg α⋅ sin β + sinα = tg α⋅ sin(9 0∘ − α)+ sin α = sin-α ⋅cosα + sin α = cos α 10- sin α+ sin α = 2 sinα = 13.

Przy tych przekształceniach korzystaliśmy z następujących faktów:

  • jedynka trygonometryczna,
  • fakt, że 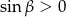sinβ > 0 (przy opuszczaniu pierwiastka),
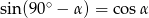  • wzór redukcyjny sin(90∘ − α) = co sα .

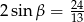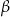Analogiczny rachunek pokazuje, że drugie z podanych wyrażeń jest równe 2 sin β = 24 13 – trzeba we wszystkich powyższych przekształceniach pozamieniać α i β miejscami. Widać więc, że drugie wyrażenie ma większą wartość.  
Odpowiedź: Drugie wyrażenie

Wersja PDF