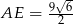/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 6540902

Dodaj do ulubionych
Dodaj do rozwiązanych

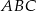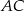W trójkącie prostokątnym ABC wysokość BD dzieli przeciwprostokątną AC na odcinki o długościach 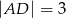|AD | = 3 i |DC | = 24 .

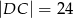  • Oblicz długości boków trójkąta ABC .
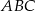  • Oblicz długość odcinka 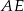AE , gdzie 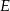E jest punktem wspólnym dwusiecznej kąta 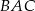BAC i boku BC .

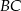Rozwiązanie

Rozpoczynamy od rysunku

PIC

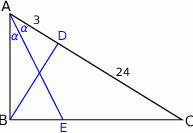
  • Z podobieństwa trójkątów 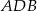ADB i BDC mamy
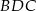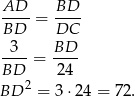
    AD-- = BD-- BD DC 3 BD ---- = ---- BD 2 24 BD = 3⋅ 24 = 72.

    Mamy zatem

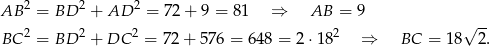
    2 2 2 AB = BD + AD = 72+ 9 = 81 ⇒ AB = 9 √ -- BC 2 = BD 2 + DC 2 = 72 + 5 76 = 648 = 2⋅18 2 ⇒ BC = 18 2.

     
    Odpowiedź: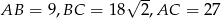 √ -- AB = 9 ,BC = 18 2,AC = 27

  •  

    Sposób I

    Aby wyliczyć długość odcinka 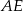AE wystarczy wyliczyć 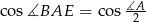cos∡BAE = cos ∡A2- . Liczymy ze wzoru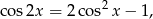

    2 cos 2x = 2 cos x − 1 ,

    który dla kąta ostrego x możemy zapisać w postaci

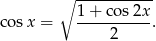
    ∘ 1-+-co-s2x- cosx = ---------- . 2

    Mamy zatem

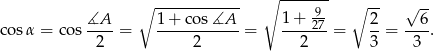
    ∘ ------------ ∘ -----9- ∘ -- √ -- ∡A-- 1-+-co-s∡A-- 1-+--27- 2- --6- cos α = cos 2 = 2 = 2 = 3 = 3 .

    Patrzymy teraz na trójkąt prostokątny ABE .

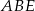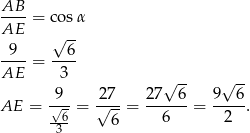
    AB-- AE = co sα 9 √ 6- ----= ---- AE 3 √ -- √ -- 9 27 2 7 6 9 6 AE = √-6 = √---= ---6-- = -2--. -3- 6

    Sposób II

    Tym razem skorzystamy z twierdzenia o dwusiecznej:

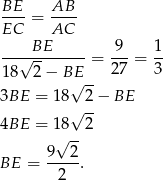
    BE AB ----= ---- EC AC ----BE------ -9- 1- 18√ 2− BE = 2 7 = 3 √ -- 3BE = 18 2 − BE √ -- 4BE = 1√8--2 9 2 BE = ----. 2

    Pozostało zastosować twierdzenie Pitagorasa w trójkącie ABE .

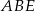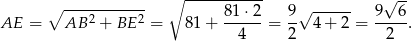
    ∘ ----------- √ -- ∘ ------------ 81 ⋅2 9√ ------ 9 6 AE = AB 2 + BE 2 = 81+ --4---= 2- 4 + 2 = -2--.

     
    Odpowiedź: √ - AE = 9-26

Wersja PDF