Zadanie nr 6548530
Dany jest trójkąt prostokątny o przyprostokątnych długości: 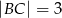 i
i 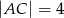 . Na boku
. Na boku 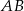 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 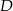 , że
, że 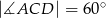 . Oblicz długość odcinka
. Oblicz długość odcinka 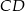 .
.
Rozwiązanie
Zaczynamy naturalnie od rysunku.
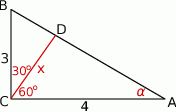
Sposób I
Korzystamy ze wzoru na pole trójkąta z sinusem.
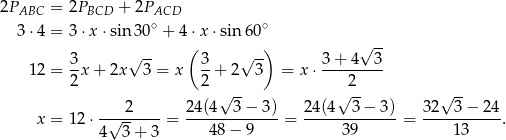
Sposób II
Tym razem korzystamy z twierdzenia sinusów. Patrzymy na trójkąt 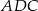 .
.
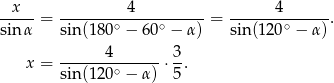
Zauważmy teraz, że
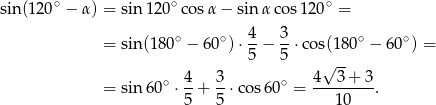
Mamy zatem
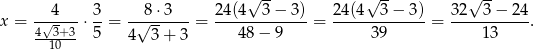
Odpowiedź: