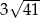/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 6881094

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie 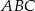ABC dane są długości boków 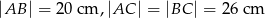|AB | = 20 cm ,|AC | = |BC | = 26 cm . Wyznacz długość środkowej BD .

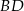Rozwiązanie

Zaczynamy od rysunku

PIC

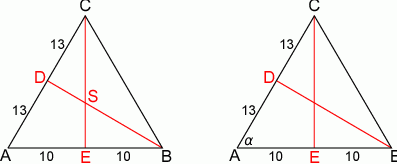
Sposób I

Ponieważ trójkąt 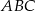ABC jest równoramienny, więc wysokość 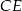CE jest również środkową. Zatem punkt 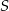S jest środkiem ciężkości trójkąta 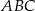ABC . Środek ciężkości dzieli każdą ze środkowych w stosunku 2:1 (licząc od wierzchołka), więc

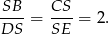
SB CS ----= --- = 2. DS SE

Ta zależność pozwoli nam obliczyć długość środkowej 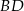BD w zależności od 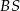BS , a długość tego ostatniego odcinka obliczymy z twierdzenia Pitagorasa.

Obliczamy najpierw długość wysokości 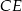CE .

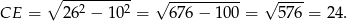
∘ ---------- √ ---------- √ ---- CE = 262 − 102 = 67 6− 100 = 57 6 = 24.

Jak już zauważyliśmy 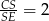CSSE-= 2 , czyli

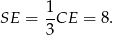
SE = 1-CE = 8. 3

Stosujemy twierdzenie Pitagorasa do trójkąta 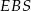EBS i obliczamy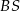 BS

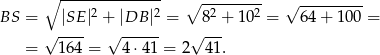
∘ -------------- ∘ --------- √ --------- BS = |SE |2 + |DB |2 = 82 + 1 02 = 64 + 100 = √ ---- √ ------ √ --- = 164 = 4⋅4 1 = 2 41.

Mamy zatem

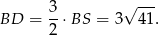
3- √ --- BD = 2 ⋅BS = 3 41.

Sposób II

Długość środkowej możemy łatwo obliczyć korzystając z twierdzenia cosinusów. Mamy

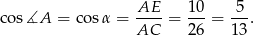
AE-- 10- -5- cos∡A = cos α = AC = 26 = 13 .

Zatem

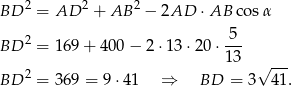
BD 2 = AD 2 + AB 2 − 2AD ⋅ AB co sα BD 2 = 169+ 400 − 2 ⋅13⋅ 20⋅ 5-- 13 √ --- BD 2 = 369 = 9 ⋅41 ⇒ BD = 3 41.

 
Odpowiedź: √ --- 3 41

Wersja PDF