/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 6889961

Dodaj do ulubionych
Dodaj do rozwiązanych

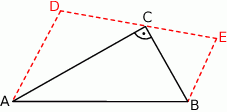
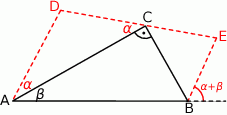
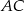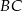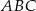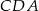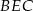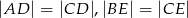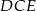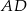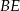Na przyprostokątnych AC i BC trójkąta prostokątnego ABC zbudowano trójkąty równoramienne CDA i BEC w ten sposób, że |AD | = |CD |,|BE | = |CE | oraz punkty DCE leżą na jednej prostej. Wykaż, że proste AD i BE są równoległe.

PIC

Rozwiązanie

Oznaczmy 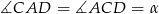∡CAD = ∡ACD = α oraz ∡BAC = β .

PIC

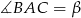Mamy wtedy

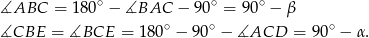
∘ ∘ ∘ ∡ABC = 180 − ∡BAC − 90 = 90 − β ∡CBE = ∡BCE = 180∘ − 90∘ − ∡ACD = 90 ∘ − α .

To oznacza, że

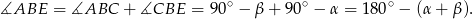
∡ABE = ∡ABC + ∡CBE = 90 ∘ − β + 90∘ − α = 180 ∘ − (α + β ).

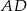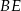To oznacza, że proste AD i BE przecinają prostą 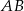AB pod tym samym kątem, czyli są równoległe.

Wersja PDF