Zadanie nr 6968535
W trójkącie 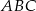 kąt przy wierzchołku
kąt przy wierzchołku 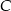 jest prosty. Trójkąt
jest prosty. Trójkąt 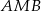 jest równoboczny. Oblicz miary kątów ostrych trójkąta
jest równoboczny. Oblicz miary kątów ostrych trójkąta 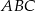 , jeśli pole trójkąta
, jeśli pole trójkąta 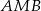 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 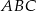 .
.
Rozwiązanie
Zaczynamy od rysunku.
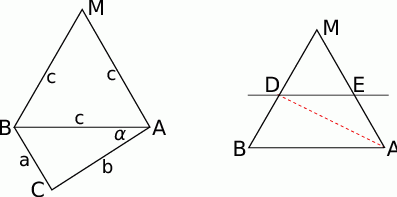
Sposób I
Przyjmując oznaczenia długości boków z rysunku, mamy
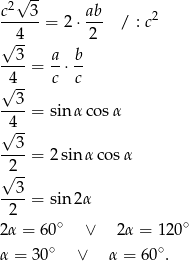
Sposób II
Tym razem postąpimy bardziej geometrycznie. Spróbujmy narysować oba trójkąty po tej samej stronie prostej 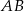 . Jeżeli przez
. Jeżeli przez 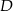 i
i 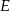 oznaczymy środki boków
oznaczymy środki boków 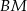 i
i 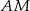 trójkąta
trójkąta 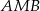 , to wierzchołek
, to wierzchołek 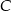 musi leżeć na prostej
musi leżeć na prostej 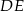 (bo pole
(bo pole 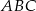 ma być dwa razy mniejsze niż pole
ma być dwa razy mniejsze niż pole 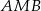 ). Ponadto kąt
). Ponadto kąt 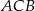 ma być prosty. Na prostej
ma być prosty. Na prostej 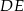 są dokładnie dwa punkty o tej własności, bo są to punkty wspólne tej prostej i okręgu o średnicy
są dokładnie dwa punkty o tej własności, bo są to punkty wspólne tej prostej i okręgu o średnicy 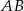 . Z drugiej strony tę własność mają punkty
. Z drugiej strony tę własność mają punkty 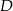 i
i 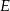 , zatem punkt
, zatem punkt 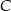 musi być jednym z tych punktów. Zatem kąty ostre trójkąta
musi być jednym z tych punktów. Zatem kąty ostre trójkąta 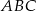 to
to 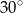 i
i 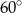 .
.
Odpowiedź: 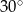 i
i