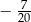/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 7020012

Dodaj do ulubionych
Dodaj do rozwiązanych

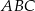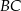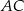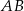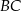W trójkącie ABC bok BC jest 3 razy krótszy od boku AC , a długość boku AB stanowi 52 długości boku BC . Oblicz cosinus największego kąta trójkąta ABC .

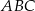Rozwiązanie

Jeżeli oznaczymy długości boków trójkąta przez 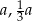1 a,3a i

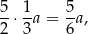
5 1 5 --⋅--a = -a , 2 3 6

to największy kąt będzie naprzeciwko boku długości a (w trójkącie naprzeciwko dłuższego boku leży większy kąt).

PIC

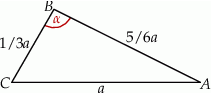
Cosinus tego kąta obliczymy z twierdzenia cosinusów.

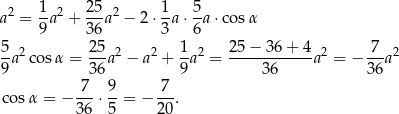
a 2 = 1a2 + 25-a2 − 2⋅ 1a ⋅ 5a ⋅cos α 9 36 3 6 5-2 25-2 2 1- 2 25-−-36-+-4- 2 -7- 2 9a co sα = 36a − a + 9 a = 36 a = − 36a 7 9 7 cosα = − ---⋅--= − ---. 36 5 20

 
Odpowiedź: -7 − 20

Wersja PDF