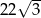Zadanie nr 7028820
W trójkącie prostokątnym 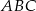 dane są
dane są 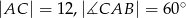 . Poprowadzono prostą równoległą do przeciwprostokątnej
. Poprowadzono prostą równoległą do przeciwprostokątnej 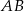 dzielącą bok
dzielącą bok 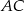 w stosunku
w stosunku 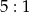 , licząc od wierzchołka
, licząc od wierzchołka 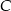 . Prosta ta przecina bok
. Prosta ta przecina bok 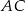 w punkcie
w punkcie 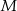 , a bok
, a bok 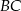 w punkcie
w punkcie 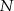 . Oblicz pole trapezu
. Oblicz pole trapezu 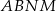 .
.
Rozwiązanie
Zaczynamy od rysunku
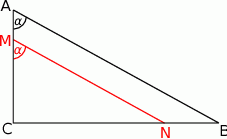
Sposób I
Widać z rysunku, że pole trapezu 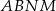 jest równe różnicy pól trójkątów
jest równe różnicy pól trójkątów 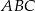 i
i 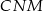 . Wyznaczamy drugą przprostokątną za pomocą funkcji trygonometrycznych
. Wyznaczamy drugą przprostokątną za pomocą funkcji trygonometrycznych
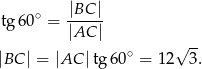
Punkt 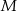 dzieli bok
dzieli bok 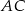 w stosunku
w stosunku 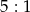 , czyli
, czyli
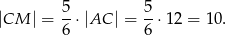
Teraz możemy obliczyć długość boku 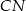
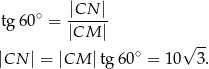
Teraz już łatwo obliczyć pole trapezu
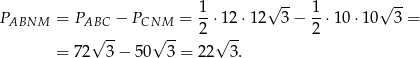
Sposób II
Tak jak poprzednio obliczamy 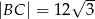 , skąd
, skąd
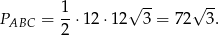
Zauważmy teraz, że trójkąty  i
i  są podobne w skali 6:5, czyli
są podobne w skali 6:5, czyli
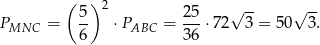
Mamy zatem
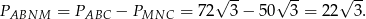
Odpowiedź: