/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 7084684

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz tangens kąta ostrego utworzonego przez proste zawierające środkowe trójkąta prostokątnego równoramiennego poprowadzone na przyprostokątne.

Rozwiązanie

Załóżmy, że przyprostokątne mają długość 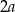2a .

PIC

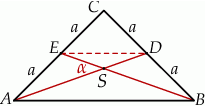
Sposób I

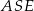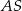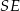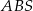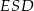Plan jest następujący. Cosinus szukanego kąta obliczymy z twierdzenia cosinusów w trójkącie ASE . Do tego będziemy potrzebować długości odcinków AS i SE . Te łatwo jednak obliczyć z faktu, że środkowe dzielą się w stosunku 2:1 (jeżeli ktoś tego nie wie, to łatwo można to zauważyć patrząc na trójkąty podobne ABS i ESD – pierwszy jest dwa razy większy od drugiego).

Liczymy. Stosujemy twierdzenie Pitagorasa w trójkącie 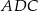ADC i mamy

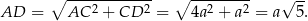
∘ ------------ ∘ --------- √ -- AD = AC 2 + CD 2 = 4a2 + a2 = a 5 .

Stąd

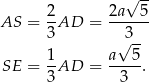
√ -- 2- 2a--5- AS = 3 AD = 3 √ -- SE = 1-AD = a--5. 3 3

Stosujemy teraz twierdzenie cosinusów do trójkąta ASE .

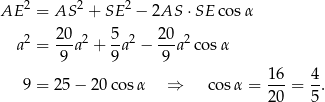
2 2 2 AE = AS + SE − 2AS ⋅SE cosα 2 20- 2 5-2 20- 2 a = 9 a + 9a − 9 a co sα 1 6 4 9 = 25 − 20 cosα ⇒ cos α = --- = --. 2 0 5

Sinus możemy obliczyć z jedynki trygonometrycznej.

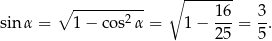
------- ∘ ---------- ∘ 16 3 sin α = 1 − co s2α = 1− ---= -. 25 5

Mamy zatem

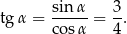
sin α 3 tg α = ----- = -. co sα 4

Sposób II

Z trójkąta prostokątnego 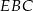EBC mamy

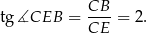
CB-- tg∡CEB = CE = 2 .

Z drugiej strony mamy

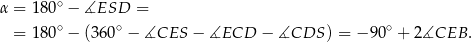
∘ α = 180 − ∡ESD = = 180∘ − (360 ∘ − ∡CES − ∡ECD − ∡CDS ) = − 9 0∘ + 2∡CEB .

Zatem

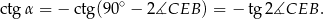
ctg α = − ctg(90∘ − 2∡CEB ) = − tg2∡CEB .

Teraz wystarczy skorzystać ze wzoru

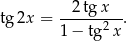
tg 2x = --2-tg-x--. 1 − tg2 x

Mamy więc

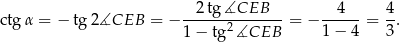
-2-tg∡CEB----- --4--- 4- ctg α = − tg 2∡CEB = − 1− tg 2∡CEB = − 1− 4 = 3.

Zatem 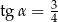tg α = 3 4 .  
Odpowiedź: 3 4

Wersja PDF