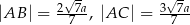/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 7170713

Dodaj do ulubionych
Dodaj do rozwiązanych

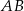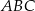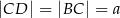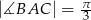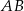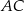Punkt D jest środkiem boku AB trójkąta ABC oraz |CD | = |BC | = a , |∡BAC | = π3- . Oblicz długości boków AB i AC trójkąta ABC .

Rozwiązanie

Oznaczmy 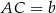AC = b i AB = c

PIC

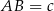
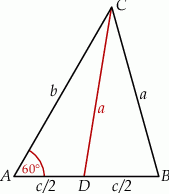
Piszemy twierdzenia cosinusów w trójkątach 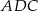ADC i ABC .

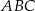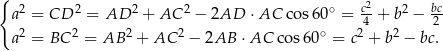
{ 2 a2 = CD 2 = AD 2 + AC 2 − 2AD ⋅AC cos60 ∘ = c4-+ b2 − bc2- a2 = BC 2 = AB 2 + AC 2 − 2AB ⋅ AC co s60∘ = c2 + b2 − bc.

Odejmujemy od drugiego równania pierwsze i mamy

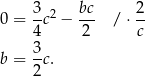
0 = 3-c2 − bc- / ⋅ 2- 4 2 c 3 b = --c. 2

Podstawiamy teraz 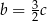b = 3c 2 do pierwszego równania układu.

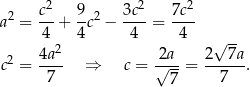
2 c2 9 2 3c2 7c 2 a = -- + --c − ----= ---- 42 4 4 4 √ -- c2 = 4a-- ⇒ c = √2a-= 2--7a-. 7 7 7

Stąd

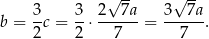
√ -- √ -- 3 3 2 7a 3 7a b = -c = --⋅------= ------. 2 2 7 7

 
Odpowiedź: 2√-7a 3√-7a |AB | = 7 , |AC | = 7

Wersja PDF