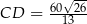/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 7258742

Dodaj do ulubionych
Dodaj do rozwiązanych

Na przedłużeniu przeciwprostokątnej 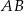AB trójkąta prostokątnego 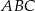ABC wybrano punkt 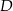D tak, że 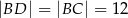|BD | = |BC | = 12 . Oblicz długość odcinka 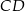CD jeżeli |AC | = 5 .

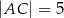Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

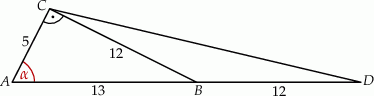
Długość odcinka 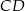CD obliczymy z twierdzenia cosinusów, ale zanim to zrobimy zauważmy, że

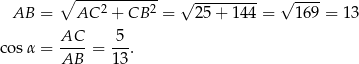
∘ ------------ √ --------- √ ---- AB = AC 2 + CB 2 = 25 + 144 = 169 = 1 3 cos α = AC--= 5-. AB 13

Stosujemy teraz twierdzenie cosinusów w trójkącie 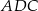ADC .

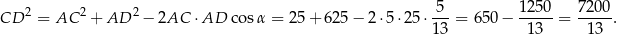
5 125 0 7 200 CD 2 = AC 2+ AD 2− 2AC ⋅AD cosα = 25+ 6 25− 2 ⋅5⋅2 5⋅---= 650 − ----- = -----. 13 13 13

Zatem

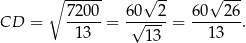
∘ ------ √ -- √ --- 72-00 6-0--2 60--26- CD = 1 3 = √ 13- = 13 .

 
Odpowiedź: 60√26 CD = 13

Wersja PDF