/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 7284302

Dodaj do ulubionych
Dodaj do rozwiązanych

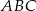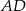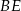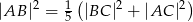W trójkącie ABC środkowe AD i BE są prostopadłe. Wykaż, że ( ) |AB |2 = 15 |BC |2 + |AC |2 .

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

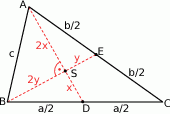
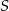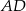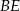Niech S będzie punktem wspólnym środkowych AD i BE , czyli środkiem ciężkości trójkąta 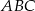ABC . Jak wiadomo środek ciężkości dzieli każdą ze środkowych w stosunku 2:1 (licząc od wierzchołka). Możemy więc oznaczyć

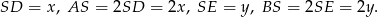
SD = x , AS = 2SD = 2x , SE = y, BS = 2SE = 2y.

Piszemy teraz twierdzenia Pitagorasa w trójkątach 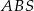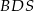ABS , BDS i ASE .

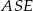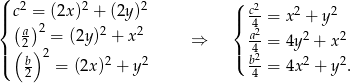
( 2 2 2 ( 2 ||{ c( =) (2x) + (2y) |{ c4- = x2 + y2 a2 2 = (2y )2 + x2 ⇒ a2 = 4y2 + x 2 || ( )2 |( 42 ( 2b = (2x )2 + y2 b4 = 4x 2 + y 2.

Dodajemy teraz do siebie dwa ostatnie równania i korzystamy w otrzymanej sumie z równania pierwszego.

a2 b2 c2 --+ ---= 5x 2 + 5y2 = 5 ⋅-- / ⋅4 4 4 4 a2 + b2 = 5c 2.
Wersja PDF