Zadanie nr 7298436
W trójkącie 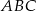 dwa kąty przy wierzchołkach
dwa kąty przy wierzchołkach 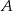 i
i 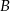 mają odpowiednio miary:
mają odpowiednio miary: 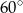 i
i 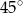 . Oblicz pole tego trójkąta, wiedząc, że długość boku
. Oblicz pole tego trójkąta, wiedząc, że długość boku 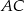 jest równa
jest równa 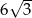 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
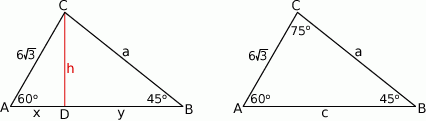
Sposób I
Dorysujmy wysokość 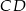 opuszczoną z wierzchołka
opuszczoną z wierzchołka 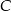 i niech
i niech 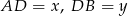 . Z trójkątów prostokątnych
. Z trójkątów prostokątnych 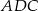 i
i 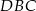 mamy
mamy
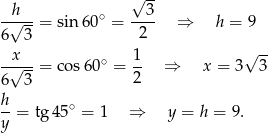
Pozostało obliczyć pole.
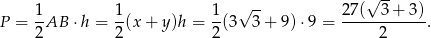
Sposób II
Tym razem skorzystamy z twierdzenia sinusów. Aby to zrobić obliczymy najpierw 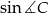 . Liczymy
. Liczymy
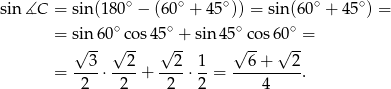
Korzystając z twierdzenia sinusów możemy teraz obliczyć długość boku 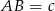 .
.
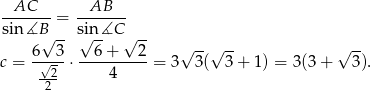
Pozostało obliczyć pole trójkąta.
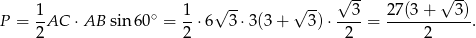
Odpowiedź: