Zadanie nr 7634632
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
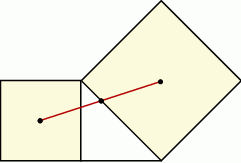
Rozwiązanie
Oznaczmy wierzchołki trójkąta przez 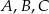 , a środki kwadratów przez
, a środki kwadratów przez 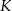 i
i 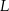 .
.
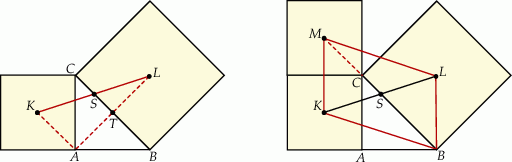
Sposób I
Dorysujmy odcinek  i oznaczmy przez
i oznaczmy przez  i
i  punkty przecięcia przeciwprostokątnej z odcinkami
punkty przecięcia przeciwprostokątnej z odcinkami 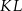 i
i 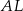 .
.
Zauważmy, że 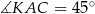 , czyli odcinek
, czyli odcinek 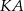 jest równoległy do
jest równoległy do 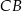 . Odcinek
. Odcinek 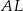 jest prostopadły do przeciwprostokątnej
jest prostopadły do przeciwprostokątnej 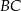 , więc trójkąty
, więc trójkąty 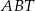 i
i 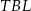 są prostokątne i równoramienne (ich kąt ostry ma miarę
są prostokątne i równoramienne (ich kąt ostry ma miarę 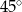 ). Zatem
). Zatem
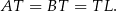
Jak już zauważyliśmy, 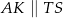 , więc na mocy twierdzenia Talesa
, więc na mocy twierdzenia Talesa
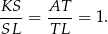
Sposób II
Dorysujmy jeszcze jeden kwadrat tak, jak na prawym obrazku i niech 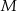 będzie jego środkiem.
będzie jego środkiem.
Zauważmy, że 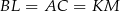 oraz każdy z tych odcinków jest prostopadły do
oraz każdy z tych odcinków jest prostopadły do 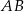 . To oznacza, że odcinki
. To oznacza, że odcinki 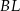 i
i 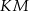 mają równe długości i są równoległe. Czworokąt
mają równe długości i są równoległe. Czworokąt 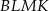 jest więc równoległobokiem.
jest więc równoległobokiem.
Zauważmy ponadto, że odcinki 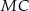 i
i 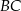 są równoległe (bo każdy z nich tworzy z prostą
są równoległe (bo każdy z nich tworzy z prostą 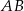 kąt
kąt 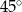 ). To oznacza, że
). To oznacza, że 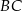 zawiera się w przekątnej równoległoboku
zawiera się w przekątnej równoległoboku 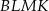 . Ponieważ przekątne równoległoboku dzielą się na połowy, mamy
. Ponieważ przekątne równoległoboku dzielą się na połowy, mamy 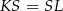 .
.
Sposób III
Tym razem skorzystamy z twierdzenia sinusów.
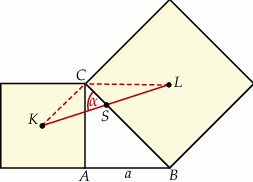
Dorysujmy odcinki 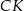 i
i 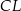 oraz oznaczmy
oraz oznaczmy 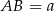 i
i 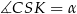 . Zauważmy, że
. Zauważmy, że 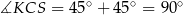 oraz
oraz 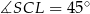 . Ponadto
. Ponadto
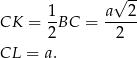
Piszemy teraz twierdzenia sinusów w trójkątach 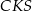 i
i 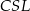 .
.
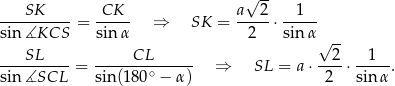
Zatem rzeczywiście 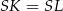 .
.

