/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 7771130

Dodaj do ulubionych
Dodaj do rozwiązanych

Trójkąt prostokątny ma boki długości 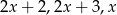2x + 2,2x + 3,x . Wyznacz x oraz promień okręgu wpisanego w ten trójkąt.

Rozwiązanie

Oczywiście największa z podanych liczb to 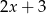2x + 3 , musi to więc być długość przeciwprostokątnej. Na mocy twierdzenia Pitagorasa mamy zatem,

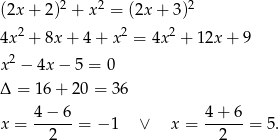
(2x + 2)2 + x2 = (2x + 3)2 2 2 2 4x + 8x + 4 + x = 4x + 12x + 9 x2 − 4x − 5 = 0 Δ = 16+ 20 = 36 4−-6-- 4+--6- x = 2 = − 1 ∨ x = 2 = 5.

Ujemne rozwiązanie odrzucamy i otrzymujemy trójkąt o bokach: 5,12,13.

Promień okręgu wpisanego możemy wyliczyć ze wzoru na pole 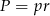P = pr , gdzie 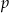p jest połową obwodu. W naszej sytuacji mamy

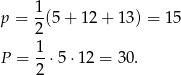
1 p = --(5+ 12+ 13) = 15 2 P = 1-⋅5 ⋅12 = 30. 2

Mamy więc

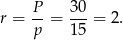
r = P-= 30-= 2. p 15

 
Odpowiedź: x = 5, r = 2

Wersja PDF