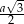Zadanie nr 7818061
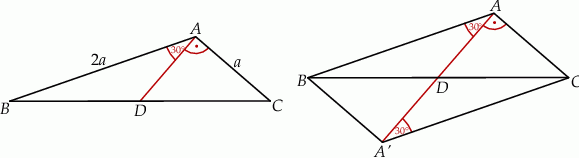
W trójkącie 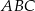 środkowa
środkowa 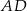 jest prostopadła do boku
jest prostopadła do boku 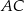 . Kąt
. Kąt 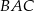 ma miarę
ma miarę 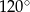 oraz
oraz 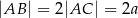 . Oblicz długość odcinka
. Oblicz długość odcinka 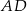 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
Sposób I
Plan jest następujący: z twierdzenia cosinusów obliczamy długość odcinka 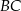 , a potem z twierdzenia Pitagorasa w trójkącie
, a potem z twierdzenia Pitagorasa w trójkącie 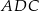 obliczamy
obliczamy 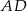 .
.
Do dzieła. Piszemy twierdzenie cosinusów w trójkącie 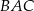 .
.
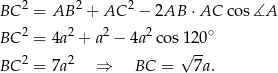
Pozostało teraz obliczyć długość środkowej 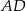 .
.
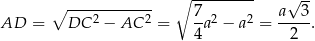
Sposób II
Niech 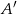 będzie odbiciem punktu
będzie odbiciem punktu 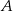 względem punktu
względem punktu 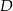 . Otrzymujemy w ten sposób równoległobok
. Otrzymujemy w ten sposób równoległobok 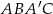 , w którym
, w którym 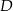 jest punktem przecięcia się przekątnych. W trójkącie prostokątnym
jest punktem przecięcia się przekątnych. W trójkącie prostokątnym 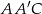 mamy
mamy
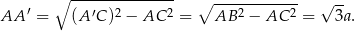
Zatem 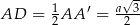 .
.
Odpowiedź: