Zadanie nr 7999789

Podstawa trójkąta równoramiennego ma długość 10, a cosinus jednego z jego kątów jest równy 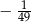− 419 . Oblicz pole tego trójkąta.

Rozwiązanie

Zauważmy, że kąt, którego cosinus podano w treści zadania jest rozwarty, wiec musi to być kąt między ramionami trójkąta równoramiennego.

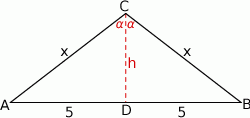
Sposób I

Oznaczmy 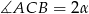∡ACB = 2α . Korzystając ze wzoru

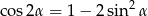
cos2 α = 1 − 2 sin2 α

obliczamy 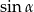sin α .

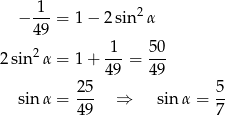
1 − ---= 1− 2sin2 α 49 2 -1- 50- 2sin α = 1+ 49 = 49 25 5 sinα = --- ⇒ sinα = -- 49 7

Patrzymy teraz na trójkąt 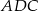ADC .

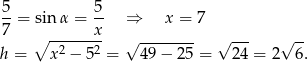
5 5 7-= sin α = x- ⇒ x = 7 ∘ -------- √ -------- √ --- √ -- h = x2 − 52 = 49 − 25 = 24 = 2 6.

Obliczamy pole trójkąta

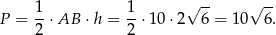
1 1 √ -- √ -- P = --⋅AB ⋅h = --⋅1 0⋅2 6 = 10 6. 2 2

Sposób II

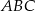Aby obliczyć długość ramienia trójkąta ABC piszemy twierdzenie cosinusów.

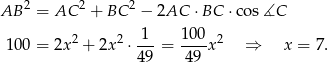
AB 2 = AC 2 + BC 2 − 2AC ⋅BC ⋅cos∡C 1 00 = 2x2 + 2x 2 ⋅-1-= 10-0x2 ⇒ x = 7. 49 49

Stąd

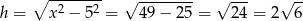
∘ -2----2- √ -------- √ --- √ -- h = x − 5 = 49 − 2 5 = 24 = 2 6

i pole trójkąta jest równe

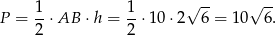
1 1 √ -- √ -- P = --⋅AB ⋅h = --⋅1 0⋅2 6 = 10 6. 2 2

Odpowiedź: √ -- 10 6