/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 8037435

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równoramiennym ramię jest 2 razy dłuższe od podstawy. Suma długości promieni okręgu wpisanego i opisanego na tym trójkącie równa się 11. Oblicz długość podstawy trójkąta.

Rozwiązanie

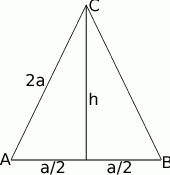
Zaczynamy od rysunku i oznaczmy długość podstawy przez a .

PIC

Korzystając ze wzorów na pole trójkąta

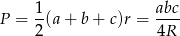
P = 1-(a+ b+ c)r = abc- 2 4R

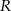będziemy mogli wyliczyć promienie r i R jeżeli tylko będziemy znali pole P . Pole można łatwo obliczyć ze wzoru Herona lub wprost, wyliczając długość wysokości 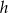h . My zrobimy to tym drugim sposobem.

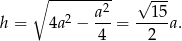
∘ --------- √ --- a 2 15 h = 4a 2 −---= -----a. 4 2

Stąd

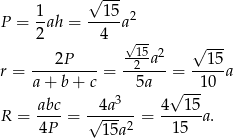
√ --- 1 15 2 P = -ah = -----a 2 4 √ -- √ --- 2P -215-a2 15 r = a-+-b-+-c = --5a--= -10--a 3 √ --- abc- √-4a--- 4--15- R = 4P = 15a2 = 15 a.

Mamy więc

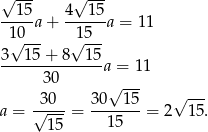
√ --- √ --- --15a + 4--15a = 11 1√0--- √15-- 3 15 + 8 1 5 --------------a = 11 30 √ --- -30-- 30--1-5 √ --- a = √ 15 = 15 = 2 1 5.

 
Odpowiedź: √ --- 2 15

Wersja PDF