Zadanie nr 8363067
W trójkącie 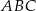 boki
boki 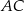 i
i 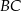 są równe. Okrąg, którego średnicą jest wysokość
są równe. Okrąg, którego średnicą jest wysokość 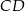 trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku 5:3 licząc od wierzchołka
trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku 5:3 licząc od wierzchołka 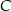 . Oblicz pole trójkąta
. Oblicz pole trójkąta 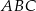 , jeżeli
, jeżeli 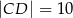 .
.
Rozwiązanie
Zaczynamy od rysunku.
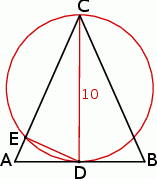
Zauważmy, że kąt 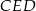 jako kąt oparty na średnicy jest prosty, więc trójkąty
jako kąt oparty na średnicy jest prosty, więc trójkąty 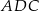 i
i 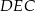 oba są prostokątne oraz mają wspólny kąt przy wierzchołku
oba są prostokątne oraz mają wspólny kąt przy wierzchołku 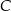 . Są więc podobne. W szczególności,
. Są więc podobne. W szczególności,
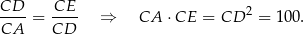
Korzystamy teraz z tego, że
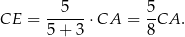
Mamy więc
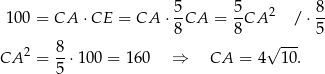
Stąd
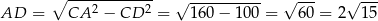
i pole trójkąta jest równe
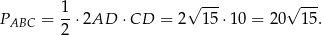
Odpowiedź: