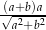/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 8398744

Dodaj do ulubionych
Dodaj do rozwiązanych

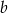Dwusieczna kąta prostego trójkąta prostokątnego dzieli przeciwprostokątną na odcinki, o długościach a i b . Oblicz długości przyprostokątnych tego trójkąta.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

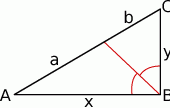
Na mocy twierdzenia o dwusiecznej mamy

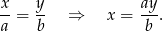
x y ay --= -- ⇒ x = ---. a b b

Ponadto, z twierdzenia Pitagorasa, mamy

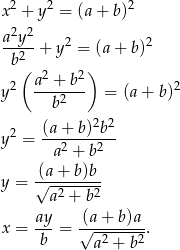
x2 + y2 = (a + b)2 a2y2- 2 2 b2 + y = (a + b ) ( a2 + b2) y2 ------- = (a + b)2 b2 (a + b)2b2 y2 = ---2----2-- a + b -(a+--b)b y = √ a2 + b2 x = ay- = √(a+--b)a . b a2 + b2

 
Odpowiedź: 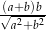√(a+b-)b- a2+b 2 i (√a+b)a- a2+b2

Wersja PDF