Zadanie nr 8459968
Przeciwprostokątna trójkąta prostokątnego jest dłuższa od jednej przyprostokątnej o 2 cm i od drugiej przyprostokątnej o 9 cm. Oblicz długości boków tego trójkąta.
Rozwiązanie
Jeżeli oznaczymy długość przeciwprostokątnej przez  to przyprostokątne mają odpowiednio długości
to przyprostokątne mają odpowiednio długości 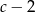 i
i 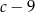 .
.
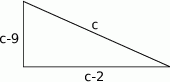
Zapisując twierdzenie Pitagorasa otrzymujemy równanie
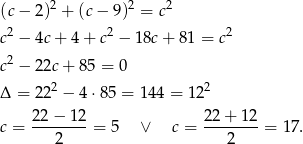
Pierwszą odpowiedź odrzucamy, bo daje ujemną długość jednej z przyprostokątnych. Zatem 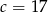 i przyprostokątne mają długości 15 i 8.
i przyprostokątne mają długości 15 i 8.
Odpowiedź: 8,15,17

