/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 8651781

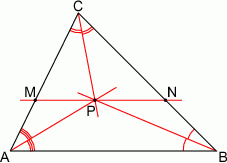
Punkt 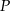jest punktem przecięcia dwusiecznych kątów trójkąta 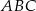ABC . Przez punkt 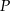poprowadzono prostą równoległą do boku 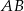, która przecięła prostą 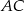w punkcie 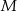i prostą 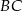w punkcie .

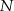Wykaż, że .
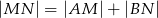Wiedząc dodatkowo, że obwód trójkąta 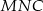jest równy 15 cm, a długość odcinka 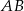wynosi 10 cm, oblicz obwód trójkąta .

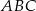Rozwiązanie

Zauważmy, że odcinek 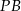przecina dwie proste równoległe, więc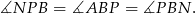
$∡NP B = ∡ABP = ∡P BN .$

Zatem trójkąt 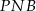jest równoramienny i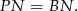

$P N = BN .$

Podobnie odcinek 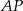przecina dwie proste równoległe, więc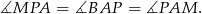

$∡MPA = ∡BAP = ∡PAM .$

Stąd trójkąt 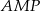jest również równoramienny i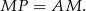

$MP = AM .$

Mamy zatem

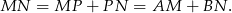
$MN = MP + PN = AM + BN .$
Liczymy obwód trójkąta 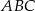korzystając z poprzedniego podpunktu.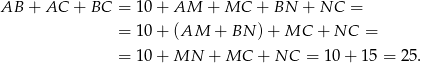
$AB + AC + BC = 10 + AM + MC + BN + NC = = 10 + (AM + BN )+ MC + NC = = 10 + MN + MC + NC = 10 + 15 = 25.$

Odpowiedź: 25 cm