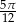/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 8874003

Dodaj do ulubionych
Dodaj do rozwiązanych

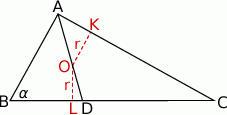
W trójkącie prostokątnym 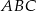ABC dwusieczna kąta prostego przecina przeciwprostokątną 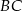BC w punkcie 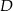D . Środek okręgu wpisanego w ten trójkąt dzieli odcinek 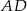AD w stosunku 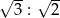√ -- √ -- 3 : 2 , licząc od punktu 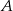A . Oblicz miary kątów ostrych trójkąta ABC .

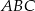Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

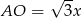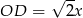Wiemy, że √ -- AO = 3x , √ -- OD = 2x dla pewnego 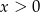x > 0 . W trójkącie 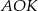AOK mamy

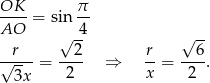
OK--= sin π- AO 4 r √ 2- r √ 6- √----= ---- ⇒ --= ----. 3x 2 x 2

Podobną równość możemy otrzymać w trójkącie 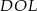DOL , ale najpierw zauważmy, że

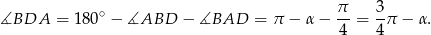
∡BDA = 180∘ − ∡ABD − ∡BAD = π − α − π- = 3π − α. 4 4

Mamy zatem (patrzymy na trójkąt DOL )

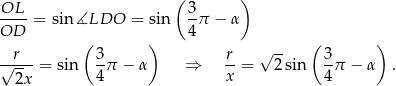
( ) OL-- 3- OD = sin∡LDO = sin 4π − α ( ) ( ) √-r--= sin 3-π − α ⇒ r-= √ 2sin 3-π − α . 2x 4 x 4

Porównując teraz r x z dwóch otrzymanych równości, mamy

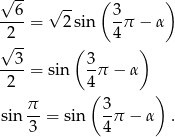
√ -- √ -- ( ) --6-= 2sin 3-π − α 2 4 √ 3- ( 3 ) ----= sin -π − α 2 4( ) π 3 sin --= sin -π − α . 3 4

Ponieważ po obu stronach mamy kąty ostre (kąt LDO jest kątem ostrym w trójkącie prostokątnym), więc

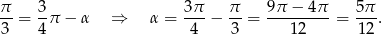
π 3 3π π 9π − 4π 5π --= --π − α ⇒ α = --- − -- = ---------= ---. 3 4 4 3 12 12

Drugi kąt ostry trójkąta ABC jest więc równy

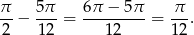
π 5π 6π − 5π π --− ---= ---------= ---. 2 12 12 12

 
Odpowiedź: 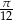-π 12 i 5π- 12

Wersja PDF