/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9086738

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójkąt prostokątny 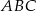ABC , w którym 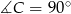∘ ∡C = 90 . W trójkącie tym poprowadzono wysokość 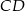CD . Wykaż, że 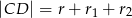|CD | = r+ r1 + r2 , gdzie 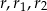r,r1,r2 są odpowiednio długościami promieni okręgów wpisanych w trójkąty 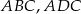ABC ,ADC i DBC .

PIC

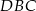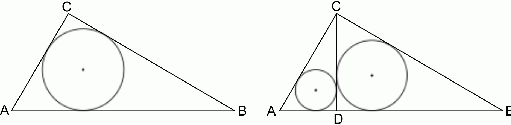
Rozwiązanie

Skorzystamy ze wzoru na promień okręgu wpisanego w trójkąt prostokątny

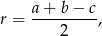
r = a-+-b-−-c, 2

gdzie 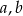a,b są przyprostokątnymi, a c jest przeciwprostokątną. Mamy zatem

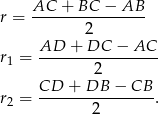
r = AC--+--BC-−--AB- 2 AD---+-DC--−-AC-- r1 = 2 CD + DB − CB r2 = ----------------. 2

Liczymy

AC + BC − AB AD + DC − AC CD + DB − CB r+ r1 + r2 = ----------------+ -----------------+ ----------------= 2 2 2 = (AD--+-DB-)-−-AB--+-2DC---= DC . 2
Wersja PDF