Zadanie nr 9120532

Przeciwprostokątna trójkąta prostokątnego o obwodzie 40 ma długość 17. Oblicz długości przyprostokątnych tego trójkąta.

Rozwiązanie

Szkicujemy trójkąt prostokątny.

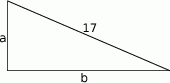
Jeżeli oznaczymy długość jednej z przyprostokątnych przez , to z podanego obwodu możemy obliczyć długość drugiej przyprostokątnej.

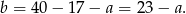
b = 40− 17− a = 23 − a.

Piszemy teraz twierdzenie Pitagorasa.

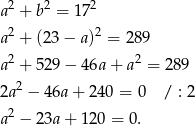
a2 + b 2 = 172 2 2 a + (2 3− a) = 289 a2 + 5 29− 46a + a2 = 289 2 2a − 46a+ 240 = 0 / : 2 a2 − 2 3a+ 120 = 0.

Rozwiązujemy otrzymane równanie kwadratowe.

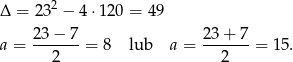
Δ = 232 − 4⋅1 20 = 49 2-3−-7- 23+--7- a = 2 = 8 lub a = 2 = 15.

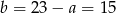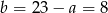Mamy wtedy odpowiednio b = 2 3− a = 15 i b = 23 − a = 8 .
Odpowiedź: 8 i 15

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz