Zadanie nr 9333853
Na boku 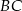 trójkąta równobocznego
trójkąta równobocznego 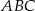 obrano taki punkt
obrano taki punkt 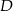 , że
, że 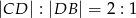 . Oblicz tangens kąta
. Oblicz tangens kąta 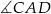 i znajdź stosunek promieni okręgów opisanych na trójkątach
i znajdź stosunek promieni okręgów opisanych na trójkątach 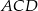 i
i 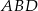 .
.
Rozwiązanie
Oznaczmy 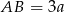 i
i 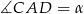 . Przy tych oznaczeniach
. Przy tych oznaczeniach 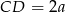 .
.
Sposób I
Aby obliczyć 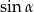 , musimy obliczyć
, musimy obliczyć 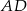 (żeby móc zastosować twierdzenie sinusów). Obliczymy długość tego odcinka z twierdzenia cosinusów.
(żeby móc zastosować twierdzenie sinusów). Obliczymy długość tego odcinka z twierdzenia cosinusów.
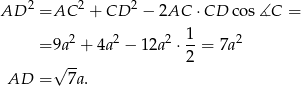
Stosujemy teraz twierdzenie sinusów w trójkącie 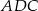 .
.
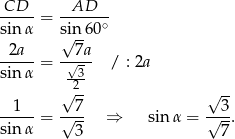
Ponieważ kąt  jest ostry, jego cosinus możemy wyliczyć z jedynki trygonometrycznej.
jest ostry, jego cosinus możemy wyliczyć z jedynki trygonometrycznej.
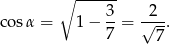
Zatem
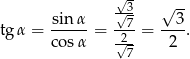
Ponieważ
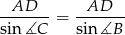
to na mocy twierdzenia sinusów promienie okręgów opisanych na trójkątach 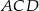 i
i 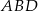 są równe.
są równe.
Sposób II
Tym razem zauważmy, że na mocy wzoru na sinus sumy mamy
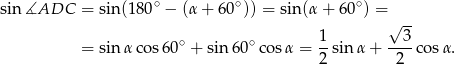
Piszemy teraz twierdzenie sinusów w trójkącie 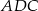 .
.
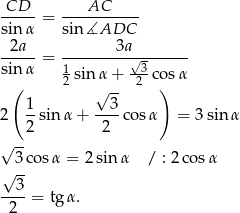
Stosunek promieni obliczamy tak samo jak w poprzednim sposobie.
Odpowiedź: 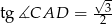 , stosunek promieni: 1
, stosunek promieni: 1

