/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9378776

Dodaj do ulubionych
Dodaj do rozwiązanych

Prosta równoległa do jednego boku trójkąta dzieli jego pole na połowy. W jakim stosunku prosta ta dzieli pozostałe boki trójkąta?

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

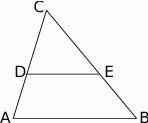
Trójkąt 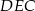DEC jest podobny do trójkąta 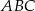ABC i jak wiemy, ma pole równe połowie pola trójkąta 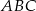ABC . Musi więc być podobny w skali 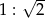√ -- 1 : 2 (bo pole zmienia się jak kwadrat skali podobieństwa). Zatem

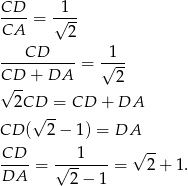
CD-- -1-- CA = √ -- 2 ----CD-----= √1-- CD + DA 2 √ -- 2CD√ =- CD + DA CD ( 2− 1) = DA CD-- = √--1----= √ 2-+ 1. DA 2− 1

Dokładnie w takim samym stosunku został podzielony bok 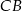CB (twierdzenie Talesa).  
Odpowiedź: 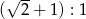√ -- ( 2 + 1) : 1 (licząc od wierzchołka)

Wersja PDF