/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9433149

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkąt równoramienny 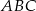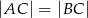ABC (|AC | = |BC | ) o długości podstawy 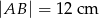|AB | = 12 cm wpisano kwadrat o boku długości 5 cm. Oblicz pole trójkąta ABC .

PIC

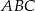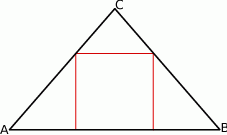
Rozwiązanie

Dorysujmy wysokość 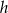h trójkąta.

PIC

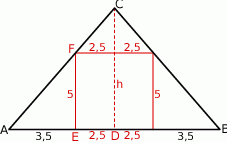
Z podanych długości podstawy trójkąta i boku kwadratu mamy

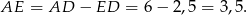
AE = AD − ED = 6− 2,5 = 3,5.

Korzystamy teraz z podobieństwa trójkątów 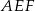AEF i ADC .

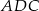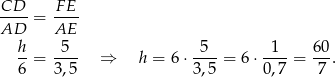
CD-- = -FE- AD AE h- --5- --5- -1-- 60- 6 = 3 ,5 ⇒ h = 6 ⋅3 ,5 = 6 ⋅0,7 = 7 .

Pozostało obliczyć pole trójkąta.

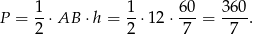
1- 1- 60- 360- P = 2 ⋅ AB ⋅h = 2 ⋅12 ⋅ 7 = 7 .

 
Odpowiedź: 360 cm 2 7

Wersja PDF