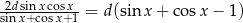/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 9446668

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równoramiennym 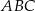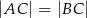ABC (|AC | = |BC | ) o kącie przy wierzchołku 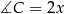∡C = 2x poprowadzono wysokość 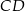CD . Wiedząc, że 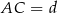AC = d oblicz odległość środków okręgów wpisanych w trójkąty 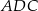ADC i DBC .

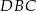Rozwiązanie

Zaczynamy od rysunku.

PIC

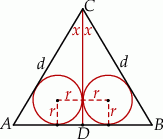
Ponieważ okręgi te są styczne zewnętrznie (bo są styczne do wysokości 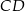CD w tym samym punkcie), to odległość ich środków jest dwa razy większa od ich promienia. Mamy ponadto

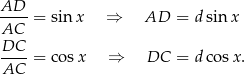
AD-- AC = sin x ⇒ AD = d sin x DC ---- = co sx ⇒ DC = d cosx. AC

Sposób I

Promień okręgu wpisanego obliczamy standardowo, ze wzoru 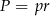P = pr na pole trójkąta 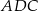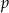ADC (p to połowa obwodu trójkąta).

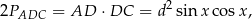
2PADC = AD ⋅ DC = d 2sin x cosx ,

oraz

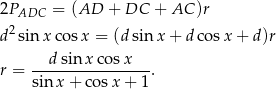
2PADC = (AD + DC + AC )r 2 d sin x cosx = (dsinx + dcos x+ d)r ---dsin-xco-sx--- r = sin x+ cosx + 1 .

Sposób II

Korzystając ze wzoru

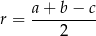
r = a+--b−-c- 2

na promień okręgu wpisanego w trójkąt prostokątny, obliczamy promień okręgu wpisanego w trójkąt 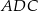ADC .

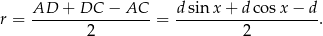
AD--+--DC--−-AC-- d-sin-x-+-d-cosx-−-d- r = 2 = 2 .

Odległość środków okręgów jest więc równa

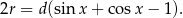
2r = d(sin x + cos x − 1).

Z ciekawości sprawdźmy jeszcze, że jest to ten sam wynik, co w pierwszym sposobie.

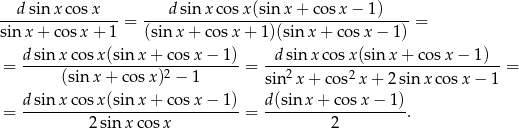
dsin xco sx dsinx cos x(sinx + co sx − 1) -----------------= -------------------------------------= sin x+ cosx + 1 (sin x+ cosx + 1)(sin x+ cosx − 1 ) d sinx cos x(sinx + co sx − 1) d sin x cosx (sin x + cos x− 1) = ------(sin-x-+-cos-x)2 −-1----- = ---2-------2---------------------= sin x + cos x+ 2sin xco sx − 1 d-sinx-cos-x(sinx-+-co-sx-−-1) d(sinx-+-co-sx-−-1)- = 2sinx cos x = 2 .

 
Odpowiedź: -2dsin-xcos-x sinx+cosx+1 = d(sin x + cos x− 1)

Wersja PDF