Zadanie nr 9558895
W trójkącie 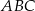 dane są długości boków:
dane są długości boków: 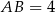 ,
, 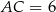 ,
, 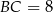 . Oblicz długości odcinków, na jakie dzieli bok
. Oblicz długości odcinków, na jakie dzieli bok 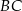 wysokość opuszczona z wierzchołka
wysokość opuszczona z wierzchołka 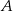 .
.
Rozwiązanie
Zaczynamy od rysunku.
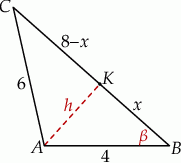
Sposób I
Do obliczenia długości odcinka 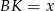 , wystarczy znać
, wystarczy znać 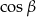 (bo
(bo 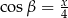 ). A ten możemy obliczyć z twierdzenia cosinusów:
). A ten możemy obliczyć z twierdzenia cosinusów:
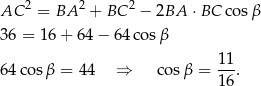
Mamy stąd
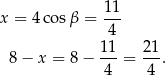
Sposób II
Tym razem obejdziemy się bez twierdzenia cosinusów. Jeżeli oznaczymy 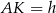 , to pisząc twierdzenia Pitagorasa w trójkątach
, to pisząc twierdzenia Pitagorasa w trójkątach 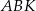 i
i 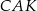 mamy
mamy
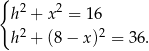
Odejmujemy od drugiego równania pierwsze (żeby skrócić 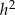 ) i mamy
) i mamy
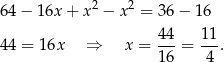
Stąd 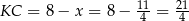 .
.
Sposób III
Tym razem zacznijmy od obliczenia pola trójkąta 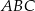 – korzystamy ze wzoru Herona
– korzystamy ze wzoru Herona
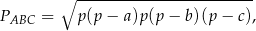
gdzie
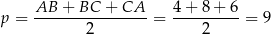
jest połową obwodu trójkąta. Mamy zatem
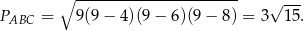
To pozwala łatwo obliczyć długość wysokości 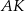 .
.
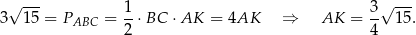
Piszemy teraz twierdzenie Pitagorasa w trójkącie 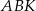 .
.
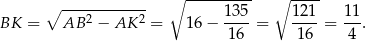
Stąd
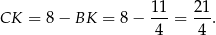
Odpowiedź: 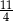 oraz
oraz